« 2006年03月 | メイン | 2006年05月 »
2006年04月28日
thesis defence
今日はアントンの thesis defence(学位審査)の発表。アントンはいまいるメンバーの中では最も古くからブザキ研にいて、多くの研究に関わってきているだけに、発表の内容はかなり濃かった。
ところで、こちらの thethis defence は、発表時間は1時間と、時間をかけておこなう。しかも、今日の発表者はアントンだけ。そういえば、僕の博士発表の時は、持ち時間はたったの 20 分だった。学部の博士候補生の全員が一堂に会し、次々に捌かれていく感じ。こちらでは、博士をひとり作るのに、大学がそれなりにお金(こっちの学生はそれなりの給料がもらえる)と時間のコストをかけて、オーダーメイド的に育てている、というスタンスが良く伝わってくる。
たとえ性能が同じでも、大量生産品とオーダーメイド品では、値段は違う。それでもオーダーメイド品が売れるのは、人の手がかけられているということ自体に、ぬくもりや安心感を感じるからである。
アメリカと日本で、社会における PhD の重みが違うのも、買い手が、そういった、人の手垢という付加価値を重要視しているからかもしれない。
充実したアントンの defence を聴きながら、そんなことをつらつらと。
投稿者 sfujisawa : 18:33 | コメント (3) | トラックバック
2006年04月24日
Nature 4/19
Weak pairwise correlations imply strongly correlated network states in a neural population
Elad Schneidman, Michael J. Berry, II, Ronen Segevand William Bialek
Retina の多細胞発火活動の統計物理的解析。pooneil さん、shuzo さんのサイトにもコメントあり。
むずかしくて、きちんと理解できたか自信がないのですが、とりあえずまとめてみます。
---
10 個のニューロンのネットワークの活動について知りたいとき、10 個のニューロンすべてに電極をさして同時記録すると、完全な情報が得られる。でも、10 個同時パッチは大変なので、2 個同時パッチをすべての組み合わせ(= 10C2 =45通)について行ったとしたら、どうだろう?直感的に考えると、いくらすべての組み合わせで 2 個パッチしたとしても、10 個同時記録をしなければ見えないような情報をかなり落としてしまっているような気がする。しかし、この論文では、10C2 回の 2 個同時記録で得られる情報量 I2 は、10 個同時記録で得られる情報量 I10 の約 90 % をカバーしている(I2/I10 ~ 0.9)ことを示している。
---
この論文のメインの主張は、大きく2つあり、
(1) 実際の retina から得られた情報パターンの分布は、最大エントロピー法より算出された分布(いわゆるボルツマン分布)とよく一致する。
(2) 最大エントロピー法による分布を考えるとき、2 つの細胞間の correlation を拘束条件として考慮したモデルが十分良い近似となっている。(3つ以上の correlation をわざわざ考えなくてもよい。)
ということです。
(1) は、統計物理では古くから知られている事実です。神経科学でも、よく応用されています。しかし、いままでは統計物からの天下りでボルツマン分布が成り立つことを仮定してから使ってたのですが、この論文では、retina ラスタープロットのパターン出現確率分布と、ボルツマン分布がよく一致していることを、実際に実験データから示しています。
(2) は、前段落で述べたような話です。
(注)この論文でいう「パターン」は、時間方向の発火パターンのことではなく、ある時間 bin でどの細胞が発火したか、という細胞番号方向のパターンです。(後述します。)
---
この論文のミソは、① Fig 1f & 2a と ② Fig 2c だと思うですが、これについて書いてみます。
実験データの解析の方法ですが、まずラスタープロットを、ある時間Δτ(ここではΔτ= 20 ms)で区切って、スパイクがあれば "1"、なければ "0" と、バイナリ化します。N = 10 個の細胞のラスタープロットを使うと、各時間 bin のデータは 10 文字の数列で表されます(Fig1b)。
fig 1f では、10 個のニューロンのラスターにおいて、ある 10 文字の数列パターンが出現する確率 (observed pattern rate (1/s): 横軸)と、もし各細胞が独立に発火すると仮定したときに計算されるそのパターンの出現確率(Approximated pattern rate: 縦軸)の関係を示しています。
たとえば、「1011001010」というパターン(cell 1,3,4,7,9 が同時に発火)を考えてみます。cell 1 の発火確率(実測値)を p1、cell 2 の発火確率を p2、・・・とします。「1011001010」のパターンが出現する確率は、p1×(1-p2)×p3×・・・(1-p10)となります。グラフから読み取ると、計算した値は約 10-8 1/s ですが、実際に観察されたのは 10-1 と 10-2 の間ぐらいです。
つまり、このパターンは実際に観測された出現率は、計算よりもはるかに高いことが分かります。
この、各細胞が独立に発火すると仮定したときに計算されるそのパターンの出現確率 inpendent model P1 は、
P1 = Πi pi (文献27の式4)
ここからが本題ですが、それでは、cell 1 の発火確率 は p1、・・・(上と同じ)で、かつ、cell 1 と cell 2 が同時に発火する確率 q12、・・・というように、2 つの細胞 i, j が同時に発火する確率が拘束条件として入っている場合、パターンの出現確率はどう計算されるか。
これは、最大エントロピー法によって求められます。結果は、
P2 = (1/Z) exp [Σhiσi +(1/2)ΣJijσiσj ] (論文の式1)
これは、いわゆる、ボルツマン分布です(※1)。これを、2次の maximum entropy distribution P2 と名付けています。
これを使って計算したパターンの出現確率 P2 と実際のパターン出現確率の関係が、Fig 2a です。(Fig 2a の青点は、Fig 1f の青点と同じです。)赤点。P1の場合と比べて、 observed と P2 がよく一致しています(←黒線上に近い位置にある)。
つまり、2 つの細胞間の関係を拘束条件として最大エントロピー法をもちいて計算されたパターン出現確率は、実験で得られたパターン出現確率をよりよく再現している、ということです。
これが、主張 (1) に相当します。
さてそれでは、cell 1,2,3 が同時に発火する確率が r123、・・・、というふうに、より高次(k 次)の同時発火確率も拘束条件として含めたらどうか?それも最大エントロピー法をつかって計算できて、すなわち k 次の maximum entropy distribution Pk です。( k = 1,2,・・,N)
高次になればなるほど、より正確に実験で得られたパターン出現確率をよりよく再現できると考えられます。
そうすると、次数が上がっていくにしたがって、どれほど正確になっていくかを知りたくなります。
そこで、k 次の maximum entropy distribution Pk が、P1 に比べてどれほど情報が増えているかを評価するために、k 次の multi-information というものを定義します。これは、(高次の)mutual information です。詳しくは文献27にあります。2次の multi-information I2 は、いわゆる mutual information です。
それで、I2/IN をプロットしたのが、fig 2a です。I2/I10 ~ 0.9 というデータが得られており、つまり 2 次の貢献度がすごく大きい、ということです。
以上が、主張 (2) に相当します。
------
(※1)
これは、Ising モデル(や Hopfield モデル)と同じです。
Ising model(Hopfield model)ではハミルトニアン H は
H = -Σ hiσi - (1/2)Σ Jijσiσj
ですが、このとき確率分布はボルツマン分布に従います。
P = (1/Z) exp (-βH)
ここで、σi は、i 番目の細胞の発火状態で、発火なら 1、非発火なら -1 です(固体物理ではスピンの向きに相当します。) Jij は、細胞 i と j の相互作用の大きさです。Z は分配関数で、βは逆温度。(この論文では温度は考慮していないので、βは出てきません。)
さて、このハミルトニアンを計算するのに、彼らは、 hi は <σi >(cell i の bin 化されたスパイクの平均発火率(出現率))、 Jij は、<σi, σj > (cell i,j の同時発火確率)の実測値を使っています。
( hi や Jij の実際の数値については、Fig 3 以降に詳しく書かれています。)
---
要するに、この論文の主張は、1 個細胞の平均発火率を hi、 2 個ペアの correlation を Jij としてハミルトニアン H を計算したときに、パターンの出現確率は、
P2 = (1/Z) exp(-H)
でよく近似できている、ということです。
結局、固体統計物理、情報統計物理の世界で発見され洗練されてきた考え方が実験神経科学でも通用するよ、ということを示した論文なわけで、面白いのは面白いのですが、本当にこの論文が nature article に相当するほどオリジナルなのかどうかは僕にはぴんときませんでした(今のところ)。
投稿者 sfujisawa : 09:43 | コメント (4) | トラックバック
2006年04月23日
カーネギー
日曜もカーネギーホールへ。このまえ、クラシック好きのカムランと話したとき、大学の ID カードがあればチケットオフィスで学生券が購入できる、という裏技を教えてくれたので、今日試してみる。普通に買うと $40 以上するチケットが、学生券では $10 均一。すごいいいじゃん、これ。さて、今日の演奏は、MET 室内合奏団で、プーランクなど。プーランクはけっこう好き。とくに声楽曲。短くて軽妙なんだけど、ふっと心にひっかかってきて、ついつい何度も聴きたくなってしまう。なんか不思議な感覚。今日のプーランクは「ピアノ・オーボエ・バソンのための三重奏曲」。これはのだめに出てきてたやつだが、これもなかなか素敵な曲。今日の演奏は、ちょっとピアノがかたかったけど、でもなかなかでした。
投稿者 sfujisawa : 11:00 | コメント (1) | トラックバック
2006年04月22日
コンサート
昨日の夜はカーネギーホールへ。フィラデルフィア響&Eschenbach のコンサートで、曲目はベートーベンの8番とマーラーの「大地の歌」(テノール Groves、バリトン Hampson)。僕はマーラーが大好きで、その中でも大地の歌は最も好きな曲。とくに第6楽章、情景が目に浮かぶかのような曲の美しさ、歌声によって表現される心の渇きと湿り、何回聴いても感動する。さて、今回フィラデルフィア響もエッシェンバッハも初めて聴いたのだが、けっこう僕の好みの演奏。ベト8も大地の歌も申し分なかった。Hampson の艶のある声も最高。ただ、バルコニーの安い席で聴いたので、声がかなり遠かったのが残念。やはり歌ものに限っては高くても一階席で聴かなきゃいかんな。。
投稿者 sfujisawa : 18:52 | コメント (0) | トラックバック
2006年04月18日
Nature AOP
今日のラボミーティングの文献紹介で使われたネタ2報。
Modulation of intracortical synaptic potentials by presynaptic somatic membrane potential
Yousheng Shu, Andrea Hasenstaub, Alvaro Duque, Yuguo Yu and David A. McCormick
McCormick ラボ。実験系は ferret の cortex のスライス。Presynaptic 側のニューロンの膜電位によって、post 側の synaptic potential (EPSP) の大きさが変化する、という論文。Pre の膜電位が浅いと、EPSP は大きくなるらしい。発想の転換だね。すごいシンプル。なんでいままで誰もやってなかったのだろう。。
メカニズムは、membrane potential が浅いほど、axon での action potential の area が大きくなる(amplitude は減少するが duration が大きくなる)、というのが原因ということらしい。(Soma と axon のダブルパッチより)。
もっとも、post側が UP だと EPSP が小さくなる(Sakmann の論文とか)ので、Pre と Post で UP-DOWN が同期してたら帳消しになるじゃん。(普通は同期してる。)なので、これが生理状態でどこまで本質的かはまだ分からない。
Combined analog and action potential coding in hippocampal mossy fibers.
Alle H & Geiger JR
こちらは海馬スライス。Mossy fiber の presynaptic terminal (mossy fiber bouton, MFB) のパッチ。
Dentate gyrus に刺激を与えたとき、Soma での membrane potential の変動が、action potential とは independent に、axon を通って passive propagation によって mossy fiber bouton まで伝達されている、という話。(これを excitatory pre-synaptic potential (EPreSP) と名付けている。)
(Menbrane potential fluctuation の axon への伝達は、上述の McCormic 論文でもやっている(Fig 4)。減衰の空間定数は、McCormic 論文では λ= 417 μm、Geiger 論文では λ= 430 μmで、ほぼ同じ。)
それで、mossy fiber bouton の膜電位が高いときは、同じ action potential でも、post-synaptic potential は大きくなるらしい。
投稿者 sfujisawa : 17:42 | コメント (1) | トラックバック
2006年04月17日
JNS 4/12
Essential Role of the Hippocampal Formation in Rapid Learning of Higher-Order Sequential Associations
Ceren Ergorul and Howard Eichenbaum
Eichenbaum ラボ。Rat で high-order の Serial reaction time 課題を開発したよ、という話。
---
Serial reaction time (SRT) 課題とは、ある sequence を覚える課題を行い(たとえば)、学習が行われたかどうかは reaction time で評価する、という課題。
この課題には、first-oeder と scond-order があり、first-order conditional (FOC) sequence は、1-2-3-1-2-3-・・のように、ある item の次にくる item が一通りに決まってしまう sequence のこと。一方、second-order conditioning (SOC) sequence は、1-2-3-1-3-2-・・のように、複合的な要素からなる。
それで、Amnesia の患者では、FOC は学習できる(reaction time が減少する)が、SOC はできないらしい (Curran 1997)。また、fMRI の研究によると、SOC では medial temporal lobe の活動が高くなるらしい (Schendan et al 2003)。それで、このような high-order sequence の学習には海馬-側頭葉系が必要なのではないかと考えられてきたようだ。
そこで、Eichenbaum は その SOC task をラットで構築して調べたよ、という話。
海馬破壊ラットと control ラットとの比較実験。
実験箱には nosepoke port(鼻をつっこむ穴)が 6 つある。正しい nosepoke port 内では reward として水が与えられる。どの nosepoke port に入ればいいかは、 port の上にある LED によって cue されている。それで、sequence のタイプは、FOC3、FOC6、SOC の 3 種類ある。
・3-item first-order conditional sequence (FOC3)
6 つある nosepoke のうち、3 つの sequence が繰り返される。(例)5-4-6-5-4-6。
・6-item FOC (FOC6)
6 つの nosepoke をすべて使う。(例) 4-2-3-5-7-6。
・second-order conditional secence (SOC)
(例) 4-5-6-4-6-5。
それぞれ、correct average reaction time (cART) と Error 数を評価。
結果はやや微妙。海馬破壊群(H-group)でも、control 群でも、SOC・FOC6・FOC3 のすべてで学習は緩やかに進んでいく(cART、Error が緩やかに減少していく)。ただし、海馬破壊群では、error が多い。面白いことに、海馬破壊群の方が、correct reaction time は短くなる。つまり、control 群は正確で遅く、破壊群は不正確で早い。この傾向は、SOC で最も強くなる、という結果。
投稿者 sfujisawa : 17:24 | コメント (23) | トラックバック
2006年04月13日
JNS 4/5(3)
A Biophysically Based Neural Model of Matching Law Behavior: Melioration by Stochastic Synapses
Alireza Soltani and Xiao-Jing Wang
昨日のつづき。
Newsome 論文では、choice probability は、Local な income を反映する、と主張しています(Newsome 論文 Fig 2)。
ここで、「grobal income」は、過去の income がすべて加算されたもの、「local income」は、Fig 2B で示されるような、時定数τをもつ leaky integrator によって過去の income が加算されたもの、を意味します。
ただ、grobal というのは τ→∞ ということなので、τが小さければ local を反映するし、τが大きければ grobal を反映する、ということになります。
それで、この時定数τを求めるのは、choice-triggered-average of rewards (CTA)を用いて調べることができます。(※)
それで、Wang モデルでは、Fig 12 で、 CTA を計算してτを求めています。
ここで、このモデルでのτは、たとえば q+ = q- = 0.06、λtot =0.1(overall biating probabiliy)のとき、τ~15 trial 程度です。
つまり、この Wang モデルでは、すごい local な income が反映されてます。
というのは、この Wang 論文のモデルでは、choice に対する報酬 / 失敗 1 回毎に、LTP/LTD が生じることを仮定しているので、過去の履歴はどんどん上書きされていってしまいます。そのために、local income を強く反映するモデルになっているようです。
ただ、τを決定するのは、1 回の LTP/LTD でのシナプス強度の変化率 q+、qq- なので、もちろんこのモデルでも q+、q- が小さければ、τはどんどん大きくなるはずです。
また、このモデルでは、A or B に selective なニューロン群はそれぞれ 1 つの population しか用意されていませんが、もし、q+ の大きさの違う2つの population があれば、それぞれ local income を表現する群と、 grobal income を表現する群の 2 つの population ができることになります。(あるいは q+ を連続的に分布させることも可能かもしれません。)
ただ、Wang 論文は Newsome 論文に即して書いているので、grobal と local については、そこまで深く議論はしていないようです。
---
(※)
Newsome 2005 J Exp Anal Behav 論文では、サルのデータから計算した CTA は、短い時定数τs と長い時定数τl で fitting できる、と主張しているそうです。
CTA(t) = ωNs exp(-t/τs) + (1 - ω)Nl exp(-t/τl)
これは、pooneil さんが指摘しているような、grobal と local の定量的な分離に相当しているのかも知れません。もっとも、その論文がダウンロードできないのですが。。
投稿者 sfujisawa : 17:03 | コメント (3) | トラックバック
2006年04月12日
JNS 4/5(2)
A Biophysically Based Neural Model of Matching Law Behavior: Melioration by Stochastic Synapses
Alireza Soltani and Xiao-Jing Wang
昨日のつづき。
このモデルでの主張の一つは、reward-dependent の synaptic plasticity を仮定することで、シナプス強度率 cA はリターン RA を表現することが可能である、という点です。
なぜかを簡単に説明します。
まず、ある chioce A に対して 報酬が与えられてたとき、sensory → A のシナプスに LTP が生じて、そのそのときシナプス強度率は
cA(n+1) = cA(n) + q+ [1 - cA(n)]
(記号は昨日のエントリーを参考。)
逆に、ある choice に対して 報酬が与えられなかったときは、 LTD が生じて、
cA(n+1) = cA(n) - q- [1 - cA(n)]
と、このように reward-dependent の synaptic plasticity を生じる、とするのがこの論文でのメインな仮定なワケです。
さてこのとき、もし target i に対する choice probability を Pi とするとき、 ci の変化率は、
Δci = q+ (1 - ci) Ii - q- ci(Pi - Ii)
steady state では Δci = 0 なので、右辺 = 0 としてごちゃごちゃと式変形すると、steady state でのシナプス強度率 ciss が求まります;
ciss = q+ Ri / {(q+ - q-)Ri + q-} 式(7)
これで、もし q+ = q- (choice 成功によって生じる potentiation 率 と 失敗によって生じる depression 率が同じ)なら、ciss = Ri となりますし、あるいは q+ = q- でない場合でも、そこまで大きく違わなければ ciss ~ (q+/q-)Ri と、Ri にたいしてリニアな関係になります。
以上が、シナプス強度率 cA はリターン RA を表現する、という主張です。
つまり、単に reward-dependent な plasticity を仮定するだけで シナプス強度率がリターンを表現するようになるわけで、つまり、biological に Return を表現するのは演算的にはそこまで難しくない、ということを示しています。
---
次に、undermatching phenomena について。
Newsome 論文の Fig 1C を見てみると分かりますが、実際のサルの choice probability は、matching の理論値よりも若干低くなっています。この現象を "undermatching" phenomena と呼ぶらしいのですが、Wang 論文のモデル系でも、この undermatching phenomena が再現されています(Fig 7)。
では、(Wang のモデル系において、)なぜこのような undermatching が生じるのか、Fig 5 で説明しています。
Fig 5 では、横軸は A に対する choice probability、縦軸は、リターン RA(赤)、RB(緑)を示しています。RA と RB が交差する点が、理論的に最適な "matching" 解です。
なぜこのような曲線になるかは、pooneil さんのサイトに mmrl さんによる詳しい解説があります。(全く同じ図が載っています。)
さて、Fig 5B では、RA、RB をそれぞれ cA、cB と置き換えています(上で述べたように q+ = q- なら Ri = ci なので)。この cA と cB を用いて、式(6)のシグモイド曲線より計算した choice probability PA (昨日のエントリ参考)が、Fig 5B の黒線で示されています。横軸の choice probability と、計算された黒線の choice probability PA が一致する点(つまり黒線と点線の交点)が、choice probability になります。
RA (cA) と RB (cB) が交差する matching 点では、cA - cB = 0 なので、黒線の PA は常に 0.5 になります(Fig 3 参照)。(というのは、黒線の PA は cA と cB の差を検出しているので。)なので、黒線と点線の交点、必ず RA と RB の交点よりも低くなります。
これが彼らの説明する、undermatching のメカニズムです。
もう少しおおざっぱに言うと、Biological なシステム(脳)では、matching を行うにあたり、(この論文のように cA と cB を用いているかどうかは分かりませんが、)おそらくリターンの「差」を検出して、そこから演算していると思われます。これが、Biological なシステム では、RA と RB が交差する点(理論的な最適点)よりも低くなる(undermatching が生じる)理由である、ということを言いたいのだと思います。
(つづく。明日は grabal と instantaneous について考えてみたいと思います。)
投稿者 sfujisawa : 19:56 | コメント (0) | トラックバック
2006年04月11日
JNS 4/5
A Biophysically Based Neural Model of Matching Law Behavior: Melioration by Stochastic Synapses
Alireza Soltani and Xiao-Jing Wang
Wang XJ ラボ。
Sugrue、Corrado、Newsome 2004 Science 論文をモデル化した論文。
この Newsome 論文は、 pooneil さんの、言わずと知れたこのシリーズに詳しいです。
Newsome 論文は、pooneil さんのまとめを引用させてもらいますと、「ある選択肢のどちらを選ぶかを決めるときに、人間や他の動物はその選択肢の持つ価値(expected value)によって選択する確率を変化させる。大脳皮質頭頂連合野のLIPニューロンはそのようなexpected valueの比をローカルな時間スケールで計算したものを表象している」ことを主張する論文です。
もう少しややこしく言うと、
LIP ニューロンの(delay-period での)発火率は、Localな income 率(Iklocal/ΣIklocal)を表現している(Newsome 論文 Fig4,5)。Newsome の主張する Local matching law では、Localな income 率は、instantaneous choice probability に等しい(Newsome 論文 Fig 2B)ので、つまり、LFP ニューロンは (instantaneous な) choice probability を表現する
というものです。
それで、今回の Wang 論文の主題は、選択行動における、return Ri、income Ii、choice probability Pi などの行動変数が、LIP 野の local curcuit でどのように表現されうるか、ということことです。この論文での彼らの主張は、LIP ニューロンが Choice probability PA を表現するような local curcuit を構築したとき、
① Choice probability PA は、シナプス強度率の差 cA-cB の関数として表現される。
② Return RA は、シナプス強度率 cA により表現される。
というものです。
---
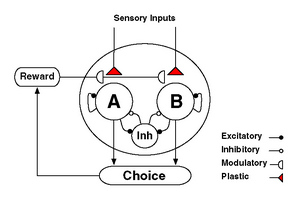
モデルの構造は以下の図の通り。(Suppl Fig1B より。)
LIP 野を仮定しています。2000 個の integrate-and-fire neuron によるモデル。
A、B と書かれているのは、それぞれ A、B (たとえば red target、green target)に selective に反応するニューロン群を示します。
仮定は、[sensory input] → [A (or B) に selective に反応するニューロン群] のシナプスに、reward-dependent に、synaptic plasticity が生じる、というものです。
このモデルによって、
(1) LIP neuron の Winner-take-all activity
(2) "undermatching" phenomana
(3) local matching law
などの現象が、シミュレーションにより再現できるようです。
この論文での記号のまとめ。
・行動変数
PA : A を chioce する確率
IA : A を選ぶことにより得られてた income (IA =(A からの Reward)/(total trail))
RA : A からのリターン(RA = IA/PA)
・生理学的変数
g+ : "UP" synapse のコンダクタンス。(g+ = 5.5nS)
g- : "DOWN" synapse のコンダクタンス。(g- = 0.5nS)
q+ : LTP phase において、DOWN synapse が UP synapse に変化する確率
q- : LTD phase において、UP synapse が DOWN synapse に変化する確率
cA : A 群のニューロンに投射するシナプスのうち、"UP"である割合。
cB : B 群のニューロンに投射するシナプスのうち、"UP"である割合。
各シナプスには 2 つの状態があり、"UP"と"DOWN"があるとします。報酬により LTP が生じるとき、q+ の確率で、DOWN シナプスは UP シナプスへと変化するとします。(LTDでは逆。)ここで、cA は、A に投射するシナプスのシナプス強度の率で、cA = 1 なら、A に投射するシナプスがすべて g+ のコンダクタンスを持ち、cA = 0 なら、すべてが g- のコンダクタンスをもつ、ということです。
---
さて、このネットワークモデルは、A、B それぞれの Recurrent による自己増幅系と、A と B の両方の入力を受けて活動する抑制系により、Winner-take-all の persistent activity が実現されます(Figure 1)。(このへんは Wang ラボお得意の話ですね。)
では、cA と cB がどのような関係にあるときに、A 群のニューロンが勝つか?
cA と cB の絶対値には関係なく、cA と cB の差によって決定される、というのがシミュレーション結果です(Figure 3)。これは、以下のような関数(シグモイド関数)で fit されるそうです;
PA = 1/{1+exp(-(cA-cB)/σ)} 式(6)
ここで PA は、A群のニューロンが"Winner"となる確率。この論文では。「A群のニューロンが"Winner"となれば choice A という行動が生じる」という仮定をしているので、PA は「A を chioce する確率」と同義で使っています。
シナプス強度率 cA、cA は、それぞれ choice A、B に対する Return を表現しています(これについては後述)。つまり、PA は、Return の差の関数として表現されることになります。
以上が、上で述べた主張①に相当します。
(つづく)
投稿者 sfujisawa : 09:48 | コメント (10) | トラックバック
2006年04月06日
Publish
以前 Cerebral Cortex にアクセプトされた論文(前のラボでの仕事)が、ようやく本 publish された。アクセプトが去年の7月だから、パブリッシュまで10ヶ月近くかかってる。。
うれしいことに、いっしょに投稿した表紙用のイラストが採用されて、今月号の CC の表紙を飾ることに。パスコ・ラキックが選んでくれたらしい。(Web ページではえらい解像度が落とされているけど、ほんとはもうちょっときれい。)
ところで、ギューリーは、ブザキラボの論文が表紙になった雑誌はぜんぶ額に入れて飾ってある。JNP や Hippocampus ではよく採用されているので、教授室の壁面は額でいっぱい。表紙になるのがかなり好きみたい。。
---
↓論文の Pdf ファイルを置いておきます。
Single Neurons Can Induce Phase Transitions of Cortical Recurrent Networks with Multiple Internal States.
Fujisawa S, Matsuki N, Ikegaya Y.
[PDF] [Suppl 1] [Suppl 2]
要約(以前書いたやつと同じ):
実験系は、海馬スライス培養切片でのパッチクランプ、Carbachol存在下。
(1) 単一細胞に10秒おきににカレントインジェクションを行ったところ、(Egorovのgraded persistent activityの実験と同じプロトコール)、細胞の発火パターンが(i)発火なし→(ii)単一スパイク→(iii)バースト発火→(iv)UP/DOWN→(v)persistent UP というように段階的に変化する現象が見られた。
(2) この現象はNetwork dependentであった。(Egorov のは Network dependent ではない。)
(3) この発火パターンの変化を「相転移(phase transition)」と見立てて、モデル化を行った。
投稿者 sfujisawa : 18:52 | コメント (0) | トラックバック
ボスの居場所
そういえば昨日今日ギューリーいないなー、と思ってたら、Ryohei さんの日記に登場してた。なるほど、いま Duke にいるのか。。
投稿者 sfujisawa : 18:50 | コメント (0) | トラックバック
2006年04月05日
Neuron 4/5
Temporal Encoding of Place Sequences by Hippocampal Cell Assemblies
George Dragoi and Gyorgy Buzsaki
ブザキラボ。ファーストオーサーのジョージは、3年ほど前に MIT の利根川ラボに移ったらしいので、僕とは在籍期間は全くかぶってない。
それにしても、ややこしくてムズいなぁ、この論文。。
かんたんにいうと、cell assmbly では、 theta 波の 1 cycle という短い時間での Sequence 表現がより精細に可能である、という話。
---
まず、theta 波の 1 cycle の中で表現される Sequence code について説明。
たとえば、論文の図1Aでは、赤色の cell とピンク色の cell では発火率のピークのある場所が約 30 cm 離れている。つまり、ラットが正の方向に進行するとすると、まず赤が発火してからピンクが発火することになるから、cross-correlation を計算すると、そのピークは 0ms からシフトするはずである。(もしラットが 60 cm/sec で走っていたとすると、約 500 msのところにピークが生じるはずである。)
一方、place cell は phase code も行っている。ラットがある place cell の place field に入っていったとき、その place cell の theta 波の中での発火位相は徐々に早い方向にずれていき(phase precession)、発火率がピークとなる場所で theta 中の位相は 180°となる。つまり、たとえば、赤色の cell が発火率ピークとなる場所では、赤色は 180°で発火し、そのときピンク色の cell はそれよりも遅い位相で発火しているはずである。ここで、赤とピンクの cross-correlation を計算すると、1theta cycle(~100ms)以内の場所に、ピークが生じるはずである。
すなわち、二つの place cell(赤とピンク)の cross-correlation を計算すると、大きいピークシフト(数百 ms 単位)をもつ山と、小さいピークシフト(1theta cycle 以内)をもつ山の、二種類の山ができるだろうことが想像できる。
それで、赤 cell とピンク cell の cross-correlation (CCG) を実際に計算したのが Fig 1D である。大きなピークシフトをもつ山(黒い線)に小さな山がのっているのがわかる。
前者を "real-time scale"、後者を "theta-time scale"でのピークシフト、と呼ぶことにする。どちらの場合でも、二つの細胞の place field の距離と、ピークシフトの大きさは、相関することが想像できる。(実際、相関している。前者は Fig 1E、後者は Fig 1G)。
ここで、後者を "theta-time scale"のほうに注目する。こちらの方は、すごい短いタイムスパンのなかで place field の sequence 性が表現されているわけで、興味深いわけです。そこで、このような、theta 波の 1 cycle の中で表現される place cell たちの発火の sequence 性を、"Sequence compression" と名付けることにする。(そしてその place field 距離とCCGシフトの相関の大きさを "Sequence compression index" と名付けることにする。)
(長々と書きましたが、以上の話はもちろんいままで知られてた話です。)
さて、このような 1 theta cycle での Sequence 表現(Sequence compression)のメカニズムは何か?① Theta pacemaker入力によって個々のニューロンが独自に phase precession を起こしているからか?(Pacemaker model)。(たとえば赤 cell とピンク cell が、お互いに全く interaction が無かったとしても、各々の細胞で phase precession さえ生じていれば、Sequence compression は必然的に生じると考えられる)。②それともplace cell 同士が cell assembly として密接に synaptic connection でつながっているから Sequence compression が生じているのか?(Assembly model)。(←Introduction 参照。)
で、どちらが本当のメカニズムなのかは今のところ分かってない。
ここまでが問題提起。
それで、そういうこと(Sequence compression のメカニズム)を調べたい、というのがこの論文の主旨なのだが、それでは何をやったか。
まず、記録した place cell の cell pair について、2つに分類する。
1trail(1lap)(つまり数十秒単位という長い時間スパン)における発火数を観測して、その発火数の変動の correlation が有意に高かった pair を 、"dependent" な place cell の pair、そうでなかった pair を "independent" な pair と分類。つまり、trail-to-trail variability がすごい似た傾向をもつ cell pair を dependentcell pair としている。
このような、"dependent" な place cell の pair では、"independent" な place cell の pair に比較して Sequence compression index が高い(Fig 3C)、というのがメインの結論。
要するに、(このような "dependent" cell pair は、cell assemble を反映しているであろう、と仮定した場合、) cell assmbly では、 1 theta cycle という短い時間での Sequence 表現がより精細に可能である、という話。(つまり、短いタイムスパンでの Temporal coding の信頼性という点では、"Pacemaker model" よりも "Assembly model" のほうが支持できる、という主張。)
問題は、この論文での cell pair の分類("dependent"と"independent"の分類)が、真の cell assembly (あるいは synaptic connenction)をどこまで反映しているか、ということでしょうね。