2006年02月17日
Multi taper (3)
昨日の続き。
なんとなく Matlab で簡単にコードが書けそうな気がしたので、試しに書いてみました。以下は、N=100 point、NW=5 の Multitaper を作るプログラムです。
|
N=100;W=0.05; for i=1:N [V,D]=eig(A); figure(1) figure(2) |
sinc 関数は matlab 関数で、sinc(t) = sin(pi*t)/(pi*t) です。t = 0 のとき sinc(0)=1 となることに注意。N が大きくなるとループ部が重たくなるので、
|
i=repmat(1:N,N,1); |
とした方がいいかもです。
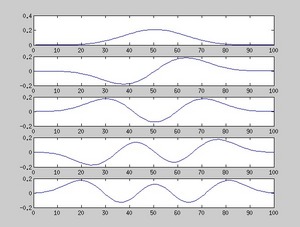
それで、固有ベクトルを固有値の大きいものから順に5つならべたのが以下の図です。Mitra 論文の Fig4 と同じ感じですね。これを窓関数として使えばいいのですね。
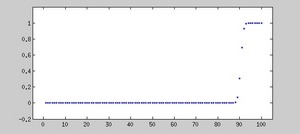
あと、固有値の分布を表示したのがその次の図です。固有値が小さい順に並んでいます。特徴は、大きいものから 2NW 番目(ここでは 2NW=10)までの固有値は、λ ~ 1 となり、それ以外は λ ~ 0 となる点です。
参考図書
Spectral Analysis for Physical Applications (Multitaper and conventional Univariate Techniques)
DB Percival and AT Walden, Cambridge Press, 1993
↑ アソハンがたまたま持ってた。Mitra 論文はこの本をベースにしてるみたい。
投稿者 sfujisawa : 20:32 | コメント (0)
2006年02月16日
Multi taper (2)
Analysis of Dynamic Brain Imaging Data
PP Mitra and B Pesaran
Biophys J , 1999,76:691-708.
昨日の続き。
ではどうやって Multi-taper を作るのか、ということだが、それは Mitra 論文の 「Analysis technique」の「Multitaper spectral analysis」という章に書いてある。しかし、この文章、省略されすぎてて何を書いてんのか理解できない。。かろうじで理解できたとこまでまとめてみます。(間違ってるかもしれません。)
--
あるデータ点数の Multi-taper の作成の仕方。
データの点数 : N
興味のある周波数領域 : [-W,W]
とする。NW=5 ぐらいになるように W を選ぶ。
ここで、(i,j) 成分が sin[2πW(i - j)] / π(i - j) である N×N 行列を Aij とするとき、
A v = λ v (論文中、式(9))
の固有方程式を解いて、その固有ベクトル v が Multi-taper らしい。
---
では、なぜ上述のような行列 Aij を選ぶのか。
(以下では、関数 v(t) をフーリエ変換したものを V(f)、関数 g(t) をフーリエ変換したものを G(f) と表記する)
Multi-taper は、スペクトルの周波数領域 [-W,W] を最適化するために設計された窓関数らしい。ここで、周波数領域で [-W,W] の矩形波関数 G(f) を考える。つまり、
G(f) = 1 (-W ≦ f ≦ W)
0 (elsewhere)
それで、
G(f) ・ V(f) = λ V(f) (λは正の整数)
を満たすような関数 V(f) があれば、この関数を窓関数として使うとき周波数領域 [-W,W] での power を最適化すると考えられる。
それで、一般的に、G(f) V(f) = g(t) * v(t) (ここで「*」は convolutionとする)という関係があるから、上の式は
∫ g(t-t')v(t')dt' = λ v(t)
と書き換えられる。ここで、g(t)、v(t) を離散値関数とすると、
Σt' g(t-t') v(t') = λ v(t)
となり、Aij = g(i-j) とすると、上述の固有方程式になる。
それで、ここがポイントなのだが、矩形波 G(f) のフーリエ逆変換は、
g(t) = sin (2πW t) / πt
となるらしいので、 Aij = sin[2πW(i - j)] / π(i - j) となる。
これででいいのかな?あんまり自信ない。
--
まあでも、上の固有方程式は Matlab なら eig 関数とかを使って簡単に解けるから、自分で multi-taper を作るのもそんなにめんどくさくはないかもね。
投稿者 sfujisawa : 19:58 | コメント (4)
2006年02月15日
Multi taper
Analysis of Dynamic Brain Imaging Data
PP Mitra and B Pesaran
Biophys J , 1999,76:691-708.
離散値フーリエ変換における Multi-taper method についての論文。
---
ブザキラボでは matlab での解析プログラムが蓄積されててとても便利である。(たとえば、ケン・ハリスがブザキラボ時代に書いたプログラム集「KenToolBox」はホームページで公開されていて、ここからダウンロードできる。)
これらのなかで、フーリエ変換を使う解析プログラムにはほぼすべてで「Multi-taper method」が使われている。(たとえば、KenToolBox にある mtpsg.m というコードでは Multi-taper を使って power spectrogram を作成する。)
これらのプログラムをただ使ってるだけなら別に問題ないのだが、先日、プログラムを少し改変しようと思ったところ、Multi-taper が何なのか分からずにつまづいてしまった。そこで、Multi-taper method について軽く勉強することにする。上の文献はアントンに教えてもらったもので、Multi-taper についての method 論文。
---
Multi-taper というのは、窓関数の一種らしい。窓関数といえば、Hamming Window とか Gaussian window とかが有名だが、Multi-taper では直交した複数の窓関数を用いる。
Multi-taper の窓関数の形は、こんな感じ(Mitra 論文の Fig4、左側の4つ)。それぞれの窓関数はお互いに直交している(つまり内積を計算すると 0 になる)。このそれそれの窓関数を使ってフーリエ変換した後に、得られたスペクトルを平均することによって、最終的なスペクトルを求める。
窓関数を使うのは、データ点数が比較的少なく、端点の影響が気になるときである。たとえば、2秒程度の長さのデータで FFT をして低周波成分(たとえば 3~8 Hzあたり)を注目するとき、どうしても端点の効果が気になる。このようなときは何らかの窓関数を用いた方が良いと思われる。データの長さが(注目する周波数に対して)とても長い場合は、べつに窓関数など用いなくてもふつうに FFT をすればよい。(窓関数に関してはこのページがけっこういい。Java が素敵。)
では普通の窓関数と比べて、 Multi-taper はどう良いのか。
<メリット(1)>
データ点数が少ないと低周波成分のデータが、どうしてもギザギザになってしまう。
たとえば、Mitra 論文の Fig5 に計算の途中経過が載っている。(Fig5 は Fig4 をそれぞれフーリエ変換したもの。)
見て分かるとおり、それぞれの窓関数で計算したデータはギザギザしてて、どれがノイズでどれが本当のピークか分かりづらい(Fig5の右側)。しかし、それぞれのデータを足しあわせて平均をとれば、ノイズ成分がとれてとても見やすくなる(Fig6)。ここで、それぞれの窓関数が直交している、というのがミソ。(直交しているからこそ、足しあわせによりノイズ成分が平坦化される。)
<メリット(2)>
窓関数を掛けてやると、端点近くでデータが0に押さえ込まれる分、power がある程度損失してしまう。しかし、Multi-taper method では、複数の窓関数を用いるために、窓関数の形に由来する Power の損失がある程度防げる。
<デメリット>
窓関数を作るのがめんどくさい。Hamming 窓や Gaussian 窓などは、自分の必要なデータ点数さえ決まればすぐに作ることができるが、Multi-taper の場合はいちいち固有方程式を解いて求めなければいけないので、自分で作ろうと思うとけっこう大変である。
つづく(かも)。
投稿者 sfujisawa : 20:54 | コメント (0)
2005年12月14日
Lisman のトーク
今日はうちのセンターのセミナーで、John Lisman のトーク。前半は、LTPにおけるシナプスメカニズムの話で、後半は記憶におけるドーパミン系の役割の話。後半の話は、半年前ぐらいに出てた Neuron の review 論文(Anthony Grace と共著)に沿った内容。ドーパミン(以下、DA)というと報酬系の話が多いが、この論文ではドーパミン系の novelty-dependent activity に焦点を当てている。
ラットを新規環境に入れる、などの刺激により、VTAのドーパミンニューロンが活性化され、これにより海馬へのドーパミン放出量が増加し、そのドーパミンが海馬のシナプス増強に影響を与えるらしい。これより、海馬 →・・・→ VTA → 海馬 というループ(論文のFig 5)が、新規情報の長期記憶形成に重要なのではないか、という仮説が考えられる、という話。
ストーリーを簡単にまとめると、こんな感じ;
(0) Anatomy。
ドーパミン系の主要な投射元は、中脳黒質(Substantial Nigra)と中脳腹側被蓋野(VTA)。主な投射先は、大脳基底核の側座核(accumbens)、線条体、および Prefrontal cortex など。海馬にも投射がある。
(1) novelty-dependent DA release in 側座核 (Legault & Wise 2001 EJN)
ラットを新規環境に入れると、側座核での DA release の増加(microdialysis で測定)。この DA release は、海馬 subiculum への TTX 適用で抑制される。つまり、海馬 dependent な現象。
(2) novelty-dependent DA release in 海馬(Ihalainen et al 1999 Neurosci lett)
ラットを新規環境に入れると、海馬での DA release の増加(microdialysis、HPLC で測定)。
(3) 海馬 → 側座核 の glu 投射が、 VTA の DA neuron の活動を活性化させる。(Grace AA 2001 JNS)
つまり、
海馬 subiculum →glu 側座核 →・・→ VTA →DA 海馬
海馬 subiculum →glu 側座核 →・・→ VTA →DA 側座核
の経路で、novelty-dependent な、海馬(&側座核)でのドーパミン放出がある。
で、このドーパミンが何をするかというと;
(4) 海馬スライス系において、Late-phase LTP は、D1 レセプター依存である。
(5) Novelty-dependent enhancement of LTP (Rowan MJ 2003 NN)
テタヌス刺激を、ラットが新規環境下にいるときに与えると、CA1 での LTP は増大する
(free-moving rat での field 記録実験)。これは、D1/D5 レセプター依存。
(6) Late-phase LTP において、DA は local protein synthesis を増強する働きを持つ(海馬分散培養系)。(Erin Schuman 2005 Neuron)
というわけで、このドーパミンは、シナプス可塑性の late-phase に効いてくる、という流れ。
ただ、このストーリー自体は、Lisman 色よりも、むしろ Grace 色のほうが強い感じがするかな。最近 Grace が、DA系と絡めた PFC-海馬 interaction の研究を力を入れてやっているのはこのストーリーとの絡みを考えているのでしょうね。
投稿者 sfujisawa : 22:54 | コメント (2)
2005年10月22日
Local cue と Distal cue
というわけで、place cell の place field 形成における、Local cue と Distal cue の役割の違いについて、最近の論文をベースに簡単にまとめてみます。
(以下の文章では、「実験部屋」は実験を行う部屋全体の空間(つまり distal cue)、「実験箱」は実験部屋の中に置いてあり、ラットがその中で課題を行う比較的狭い空間(つまり local cue)をさします。)
(1) Knierim 2004 Nature の実験:
ある実験部屋(distal cue)とある実験箱(local cue)の組み合わせで、ラットに場所を学習させる。ここで、実験箱を実験部屋に対して反時計回りに何度か回転させる。このとき、place field が反時計回りに回転していれば、その place cell は local cue をコードしており、、place field が時計回りに回転していれば、その place cell は distal cue をコードしているのがわかる、という実験ロジック。Place field が Local cue と Distal cue のどちらに引きずられるか、ということですね。
実験結果は、
CA1では、Local 14.3% Distal 12.9%
CA3では、Local 51.5% Distal 7.7%
つまり、CA3では、かなりの place cell が local cue をコードしていることが分かる。CA1では、Local でも Distal でもない(つまり、place fieldがなくなったり、ぼやけたり、新しくできたりした) place cellがけっこう多い。
(2) Moser 2004 Science の実験:
Moser 2004 science の論文でも、Knierimの実験に近い結果が得られている。
実験箱Aから実験箱Bの変化に対して(実験部屋は同じ)、CA3は place field が overlap することが少ないが、CA1は place field が overlap することが多い、という結果。解釈としては、① CA1が distal cue で、CA3が local cue、あるいは、② CA3のほうがCA1よりも、 pattern separation 能力が高い。
(3) Moser 2005 Science の実験:
このエントリー参考。実験部屋(Distal cue)は同じで、実験箱(Local cue)を変えた場合、一見、place cellのコードする領域が変わったように見えるが、実は発火数が変わっているだけで、コードしている領域は同じだ、というないよう。(CA1&CA3野)。つまり、Local cueは発火数、すなわち"Gain"によってコードしている、という解釈。(昨日のトークで、Moserは、場所の変化に対して発火数のみ変わるものを"Rate remapping"、Place field と発火数の両方が変わるものを"Grobal remapping"と名付けて、これらの違いが生じる回路的なメカニズムについていま研究しているみたいなことを言ってました。)
(4) O'Keefe 2005 Science の実験:
O'Keefeの実験では、丸い実験箱を徐々に四角い実験箱に変えていったら、place cell の place field は、ある時点で、不連続に、丸い空間の place field から四角い空間の place field へ遷移するという結果が得られている。つまり、丸と四角の中間の空間であっても、丸い空間か四角い空間のどちらかに認識されているということですね。つまり、アトラクターが存在する、というわけですね。
ここで、実験箱を Local cue と考えると、実験は同じ実験部屋でやっているので、CA1は完全にLocal cueをコードしていることになる。
(ギューリーはことあるごとにこの論文を絶賛していますね。丸い空間と四角い空間で完璧にplace fieldが分離されてるのがすごい、と。ところで、このようにplace fieldが完全に分離されるにはどれくらい時間がかかるのでしょう?この論文のMethodをみてみると、だいたい1週間と書かれています。でも実際は、Pre-trainingをもう少し長い時間やっているかもしれないですね。O'Keefe Nature2002では、円形箱と四角型箱で完全に place field が分離するのに20日近くかかっていますからね。Moser実験とのデータの違いも、この辺のPre-training時間にあったりするのかもしれないです。)
(5) Moser 2005 Neuron の実験:
これはおととい書いたやつですね。O'Keefeと同じく実験箱を円形→四角形に変形させていったら、O'Keefeのように一気にplace fieldが遷移する細胞と、そうではなく徐々にplace fieldが変形していく細胞の両方が存在する、という結果。
昨日のトークでも話してたのですが、徐々に変形する細胞がいるからと言って、アトラクターの存在を否定するわけではない、と主張していました。というのは、このような細胞も、円形から四角形に変形していくときと、四角形から円形に変形していくときでは、place fieldの遷移の仕方が違うというデータが得られているので(Fig4(CA3)&Fig6(CA1))、つまり、「ヒステリシス(Hysteresis)」が存在する、というわけです。(ヒステリシスが存在するということは安定点の存在を示唆しますよね。)(ヒステリシスは電磁気学や固体物理学などでよく出てきますが、入力に対する応答がその履歴に依存しているということです。直感的な図(ハーマン・ハーケンの本より))
--
さて、Local cue と Distal cue が CA1細胞の place field に与える影響をまとめると、
Moser-McNaughtonの考え方では、CA1では、
Local cue は、place cell の、place field は変えずに発火数(gain)を変える。
Distal cue は、place cell の、place field そのものを変える。
O'Keefeの考え方では、CA1では、
Local、Distal に関わらず、place field が変化する。
で、Contradictoryである。(というのがギューリーの解釈)
もっとも、O'Keefeの実験で使っている実験箱は、かなり大きい(一辺 102cm、高さ77cm)。(ちなみにMoserのは、一辺 80cm、高さ50cm)。もしラットの視界に入ってくるものが実験箱の壁面だけで実験部屋が見えないなら、実験箱を local cue と考えるのはおかしいかもしれない。
そうしてみると、Local cue / Distal cue という単純な分類ではダメなのかもしれませんね。(ギューリーは、Local cue、Distal cue と言う言葉を好んで使うんですけど。)Distal cue はむしろ「Context」と言い換えた方がいいかもしれないですね。Moserの実験ではラットは実験部屋をContextとして認識してて、O'Keefeの実験では実験箱をContextとして認識しているのかもしれない。
あんまりうまくまとまりませんでしたね。またそのうち蒸し返してみます。
投稿者 sfujisawa : 20:49 | コメント (0)
2005年10月21日
Moserのトーク
ちょうどタイムリーなことに、今日の夕方、コロンビア大の Medical campus で Moser夫妻のトークがあったので、聞きに行ってきました。
May-Bitt Moser(妻)のほうが Entorhinal cortex の "grid cell" について。話のメインは、彼らの Nature 2005 でしたが、何個かNewのデータも入ってました。
ここで、簡単に "grid cell"の特徴についてまとめてみると、
(1) grid cell の place field は等間隔にgrid状に存在する。gridの間隔は30~50cmと、比較的広い。gridの交線はだいたい 60°で一定。(Nature 2005 Fig1-2)
(2) 大きい実験箱にいるときも小さい実験箱にいるときも、grid の間隔は変わらない。(Fig1)
(3) grid cellは、ECのII/III層だけではなく、V/VI層にも存在する(New)。(II/III層が海馬へのInputで、IV/Vそうが海馬からのOutputであることを考えると、入出力のどちらにもgrid cellがあることは少し不思議な感じがしますね。)
(4) 各層で、層の深い方に行くほど、grid間隔の大きい細胞が多い。(Fig2)
(5) lacal cueの位置をずらすと、gridもそれにつれられてずれる。(Fig4)
(6) 暗い環境に変えても、gridは保持される(Fig5)
(7) 新規環境でも、1分ぐらいでgrid状の place field が形成される。(Fig6)
(8) 同じgrid cellで、同じ環境であれば、gridの位置は、trialごとに変化することはなく、安定している。
(9) しかし、同じgrid cellで違う環境の場合(例えば円形の実験箱と四角形の実験箱)、gridの間隔は変わらないが、gridの位置が少し(10cmぐらい)シフトする。(New)
(10) ECには、grid cell意外にも、head directionに反応する細胞もある。II/IIIではgrid cellの方が比較的多いが、V/VI層ではhead direction cellの割合の方が多くなる。(ちなみに、head direction cellはsubiculumにも多いことが知られています。)
で、Moser妻は、このような place fieldは、① Landmark-basedに形成されるのか、あるいは② Self-motion-basedに(つまりpath integration)によって形成されるのか、ということをdiscussionしていました。上述の(2)や(6)や(7)のデータからは、path integrationかと考えられるが、(5)のデータからするとLandmark-baseなので、まだ何とも言えない、という結論でした。それにしても、やっぱり面白いですね、grid cell。海馬の入力もとであるECにこんな細胞があるとは、ほんとに驚きです。
次に、Moser旦那の方は、海馬CA1、CA3、DGやECでのplace fieldのremappingの話など。話のストーリー的には、海馬ではどこで pattern separation と pattern cmpletion が行われているか、という内容。
メインの話は、彼らの Science 2004a,2005(参考)、Neuron 2005(昨日のエントリー参考)とかでした。
面白かったのは、DGでも、Neuron 2005の円形の実験箱と四角形の実験箱への7段階変形の実験をやっていて、DGでは、2段階目か3段階目ぐらいでplace field が変化してしまう、というデータ(unpublished)。つまり、DGはpattern separationの機能が強い、とMoserは述べてました。
ところで、以前ギューリーがラボミーティングの時に話してたのですが、Moserのラボにはテクニシャンが7人もいるらしいですね。ノルウェーの研究界のホープらしくて、研究費をばんばんもらっているらしい。その話をしてるとき、うちのラボの誰だったかがギューリーに質問。「なんでうちのラボにはテクニシャンがひとりもいないんですか?」ギューリーの答え「テクニシャンが全部やってくれたら、おまえらポスドクの勉強にならないからだよ。」 うーん。。
投稿者 sfujisawa : 20:27 | コメント (0)
2005年10月14日
PCAとSVD
ブザキラボと、隣のケン・ハリスラボ(ケンはブザキ研出身なのでラボどうし仲がよい)は、数物系出身の理論家が多い。全体の1/3ぐらいが理論家かな。解析系のプログラムなどは、理論系の人がバリバリ書いてくれる。実験系の人は、プログラムの使い方は分かるが、しかし原理まではなかなか勉強できない。それで、ハリスラボのポスドクのカリーナ(彼女は数学出身)が実験系の人のために、解析用の数学を簡単に説明してくれる勉強会を毎週金曜にしてくれているらしい。その勉強会の存在を先日知ったので、今回から僕も参加させてもらうことにする。
今日のお話は、PCA(principal component analysis:主成分分析)と SVD(Singular Value Decomposition:特異値分解)の違いについて。カリーナが講義室で黒板を使って30分ぐらいで説明してくれる。
さすが数学出身だけあって、話がシンプルですごいわかりやすかった。内容を全部書きたいところだけど、webで数式を書くのは大変なので、省略してまとめてみます。(mimetexとかを入れればいいんだろうけど、入れ方が分からない。。)
N次元のデータが、n個あったとする(ただし、n >= N )。すなわち、
y1 = (y11, y12,・・・, y1N )
y2 = (y21, y22,・・・, y2N )
・・・
yn = (yn1, yn2,・・・, ynN )
この、n行N列のデータ行列を A とおくとき、A の共分散行列は、
AT A
で求められる(詳細は省略)。PCAは、この AT A の固有値問題に帰着される。
で、SVDは、行列 A に対して、 結局 AT A の固有値問題に帰着されるらしいので、要するに、PCAとSVDは同じことらしい。
AT A は当然 N×N の対象行列になるので、N個の非負固有値が存在するはずで、固有値問題が解けるわけですね。
ここまで分かれば、matlabで簡単にPCA解析できますね。普通に固有値・固有ベクトルを求める eig 関数を使ってもいいし、svdという関数があるのでそれを使えばもっと簡単ですね。
例えば、Aをn行N列のデータ行列とするとき、
[U,S,V] = svd(A);
と入力すると、A=U S VT となるよう特異値分解してくれて、これはPCAを行っているのと等価なわけですね。(なんと一行でPCAができてしまう!)ここで、V は主成分結合係数ベクトルを並べた行列。データ行列を主成分軸の張る空間に移したければ、A*V(あるいは U*S)で計算できますね。
(↑これで正しい?)参考ページ。
投稿者 sfujisawa : 22:52 | コメント (0)
2005年10月13日
脳波メモ
前回のラボセミナーはアントンのJournal clubで、Tononiのこの論文を紹介したのだが、脳波の話になると、俄然ギューリーが興奮してくる。とくにこの論文では、Fig2の覚醒下でのTMS-responseを見て、「これは単なるalpha波のリセットじゃねーのか」と声高に主張していた。(Fig1でalpha波がきれいに見えている(つまり覚醒下で目をつぶっている状態)のが理由。)まあ、それはともかくとして、ギューリーは脳波(やLFP)の話になると話が止まらなくなる。どうやら重度の「脳波マニア」みたい。話を聞いてるだけで勉強になって面白いのですが、話がマニアックになるとついていけなくなってしまうので、少し僕も勉強することにしました。
今回は、NonREM睡眠時でのCortexで見える脳波についてまとめてみました。
(1) Slow oscillation: <1 Hz, generally 0.5~1 Hz
発生源:Neocortex。
理由(i) thalamusを切除してもcortexでslow oscillationが残る。[Ref]
理由(ii) cortexを切除すると、thalamusではslow oscillationが消える。[Ref]
(いわゆるUP-DOWN stateは基本的には麻酔のartifactと考えられていますが、脳波的にはslow oscillationに対応すると考えればいいと思います。)
(2) Spindle: 12~15Hz (Human), 7~14 Hz(Cat), Rat ~14 Hz(Rat)
発生源:thalamic reticular (RE) neuronがペースメーカー 。[Ref]
ただし、広域でのspindleの同期には、Neocortexが必要。[Ref]
(3) Delta: 1~4Hz
発生源:thalamus起源(thalamocortical neuron)とneocortex起源の2種類ある。
端的な模式図がありました。
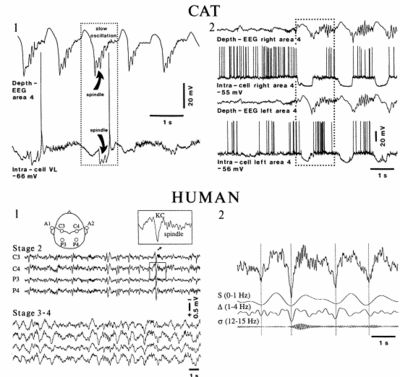
Steriade の Neurosci 2000のFigure8をぱくりました。(Steriade先生、すいません。。)
上図はCatのintra/extra記録と、humanのEEGを比較したもの。
Slow oscillationは、NonREM中で、intra記録でUPからDOWNに遷移するときに、extra記録で上向きに観察されている波。この図では、Slow oscillationの後にspindleが続いている。(この、slow oscillation-spindleのペアは、よく観察される。)
Human(scarp)でのEEG記録では、slow oscillationはNREM時に下向きの(この記録では下向きが+らしい)大きな波として観察される。(これを、別名K-complex(KC)というらしい。)NREMのStage2ではslow waveにspindleが続くのが観察され(KC/spindle)、NREMのState3~4ではslow waveにdeltaが続くのが観察される(KC/delta)。(脳波による睡眠 stage の分類(ヒト)の一覧表は、このページにありました。)
Steriadeによる、slow wave (K-complex)、spindle、delta波の生成メカニズムの模式図。
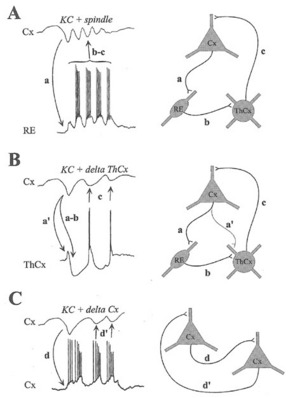
Steriadeの本のFig3.43をぱくりました。
ところで、Slow oscillationが初めて記述されたのは、1993年と結構新しい。それ以前までは、Slow wave(徐波、4Hz以下の波)として一緒にされていた。Steriadeの1993年の論文(ネコのintra記録でslow oscillationを発見し、ヒトEEG記録で確認)により、slow oscillation (<1Hz)とdelta (1-4Hz)がはっきりと分けられるようになる。
さて、ほんとは、Cortex/Hippocampus間やCortex/Cortex間での脳波の同期・伝播や、脳波リセットなどについて(とくに覚醒下と睡眠下での違いなど)を書きたかったのですが、今日は疲れたのでまた今度まとめてみます。
*以上のまとめは以下の本の3.2節を参考にしました↓。Steriadeも重度の脳波マニア。
Neuronal Substrates of Sleep and Epilepsy、Mircea Steriade (Cambridege Press, 2002) サンプル
(ところで、Amazonでこの本のカスタマーレビューを書いているbrainfreakさんって、なんとなくpooneilさんのような気がするのですが。。気のせい?)