« 2006年01月 | メイン | 2006年03月 »
2006年02月28日
Nature AOP
Reverse replay of behavioural sequences in hippocampal place cells during the awake state
David J. Foster and Matthew A. Wilson
マチュー・ウィルソン。ラット、Place cell ネタです。
今日のラボミーティングの文献紹介で取り上げられたので、ここでも取り上げてみます。
この論文では、Place cell の 発火 sequence が、 ripple 中で逆順になって圧縮される、という驚きのデータを報告しています。
もう少し丁寧にいうと、place cell a が 場所(領域)A をコードしていて、place cell b が場所 B、・・・をコードしているとします。このとき、ラットが場所 A → B → C → ・・・と走ると、Place cell は a → b → c → ・・・という順番で発火することになります。それで、この論文では、ラットが休止しているときに生じている ripple 波の中で、place cell が、・・・→ c → b → a のように逆順に発火する、というものです。しかも、ripple は時間的には 100ms 程度の短いものなので、Sequence は時間的に圧縮されていることになります。
ウィルソンが有名になったのは、おそらくこの論文(Wilson & McNaughton 1994)からだと思うのですが、この以来、ウィルソンは睡眠中での place cell の発火の再現とその Sequence 性にこだわった研究を続けています(Louie & Wilson 2001、Lee & Wilson 2002 など。)ただ、これらの論文では、Sequence の再現は、順方向であると主張しています。Lee & Wilson の Figure 6 に Slow-wave sleep 中の ripple での Sequence 発火が載ってますが、これは順方向です。睡眠中と休憩中での ripple 発生メカニズムがそこまで大きく違うとは思えないのですが、なぜ順方向と逆方向の違いが出てくるのかは今後明らかにしていかないといけないところでしょう。
---
Sharp Wave / Ripple のおさらい。
Sharp wave とは、~100 ms 程度の幅をもつ鋭い波のことで、ripple は 200 hz 程度というとても高い周波数を持つ波です。Sharp wave と ripple は同時に見られることが多いので、Sharp wave / Ripple とよくまとめられます。
実際の波形はこんな感じです。画面真ん中ぐらいにぽこっと上向きにとんがっているのが Sharp wave で、それに乗っている高周波成分が ripple です。(画面は全体で 800 ms)。
Sharp wave/Ripple は、ラットが動いていないとき、および Non REM 睡眠中に観察されます。つまり theta 波が発生していないときです。(ただしこの論文に注意。)Ripple 中では発火数が上昇します。また、ripple 発生源は海馬 CA3-CA1 ネットワークらしいです。
以上の Ripple の特徴より、Behavior 中での place cell の発火活動が、休憩時(海馬への入力が少なくなっているとき)に海馬内で形成される ripple 波により圧縮再現され、これが plastisity を生じさせ、memory consolidation を形成するではないか、という仮説が考えられてきました。
この Ripple 圧縮仮説は、もともとはギューリーがむかし提案したものみたいです(Buzsaki, Brain Res 1986, Neuroscience 1989)。
それで、今回の Wilson 論文では ripple 波により圧縮再現が実際に生じている(ただし逆順で)ことを実験で示したわけですね。
ところで、この Wilson 論文でも、Buzsaki 1986、1989 を引用はしているのですが、彼らは、単なる ripple の説明のところで引用していて、ギューリは「引き方が違うョ!」と言って憮然としてました。。
投稿者 sfujisawa : 23:14 | コメント (0)
2006年02月27日
Nature Neurosci 3月号
The tempotron: a neuron that learns spike timing-based decisions
Robert Gutig & Haim Sompolinsky
Sompolinsky は、以前は Hopfield model などをやっていた理論家です。今回は「Tempotran」という新たな Machine learning を開発した、という話です。
Temporoton では、N 個のニューロンの発火パターンを識別するみたいです。つまり、パーセプトロンに時間情報が入ったみたいなものかな。
識別は、出力ニューロンが時間内に1回以上発火するかどうかで判定します。Fig 1a でいうならば、黒のラスタープロットの入力では出力ニューロンは発火を生じ、灰色のラスターでは発火を生じません。
--
Temporoton では、ある1つのニューロン(出力ニューロン)が、N 個のシナプスの入力を受けているとします。出力ニューロンは、Integrate-and-Fire ニューロンで、
V(t) = Σi ωi Σti K(t - ti) + Vrest (論文中式1)
ωi は i 番目のシナプスの結合強度、K(t) は Postsynaptic potential を表すカーネル関数(Fig1C参照)。
それで、時間 0 から T まで、N 個のシナプスから spike train を入力したとき、出力ニューロンが発火するかどうかでその入力パターンを識別します。
では、学習はどうするか。(Fig 2)。
ある覚えさせたい入力パターンを入力したときに、出力ニューロンの膜電位 V(t) が高かった時間点を tmax を調べます。もし V(tmax) が閾値 Vthr を越えていたら、そのままにします。もし、越えていなかったら、越えるようになるように、シナプス強度 ωi を変更します。
Δωi = λ Σ K(tmax - ti) (論文中式2)
つまり、tmax から時間的に近くに入力があったシナプスのシナプス強度が強くなるよう学習させます。
記憶できるパターンの数は、シナプス数 N の2倍ぐらいだそうです。
---
論文では出力ニューロンの数は1個でしたが、もし出力を M 個にすると、N 入力 M 出力の simple perceptron に似てきます。
では、この Tempotronがパーセプトロンに比べてなにが新しいかというと、
・時間情報を含めたパターンの分離ができる
・演算に Integrate-and-Fire neuron を使っているので、より生理状態に近い。
というところでしょうか。
ただ、問題点としては、
・学習方法ががなんとなく不自然な感じをうける。
・パーセプトロンにくらべて一般性に乏しい。
などが挙げられると思います。
この Tempotron が今後はやるかどうかは、微妙なところかな。。
投稿者 sfujisawa : 21:09 | コメント (0)
2006年02月24日
大規模シミュレーション
Izikevich は、ニューラルネットのアトラクターなどをやっている理論家ですが、彼のホームページでは彼の本などの著作をダウンロードできたりするので、たまにチェックしてます。それで今日、彼のホームページをひさびさに見てみたら、また面白いことをやってました。1011 のニューロン(1015 のシナプス)をもつ thalamocortical network のシミュレーションをやっているみたいです。。 Movie も載せてました。(なんかセルオートマトンの "Life Game" を想像させます。)1 秒分のデータを得るのに、3GHz のプロセッサーを27使って、50日かかるらしいです。しかも、このネットワークサイズになるとシナプス結合行列を記憶させるだけで1万テラバイトのメモリーが必要で、しかしそのようなメモリースペースが準備できないために、計算 1 step 毎にシナプス結合行列を再構築してるらしいです。。
投稿者 sfujisawa : 20:32 | コメント (0)
2006年02月22日
Nature 2/22
Efficient auditory coding
Evan C. Smithand Michael S. Lewicki
声音などの音の波形は、けっこう複雑な形をしている。
でももし、音の波形が、何個かの関数の足し合わせで表現できたとすると、音を情報として伝達するのに都合がよい。
つまり、音の波形 x(t) を、ある kernel function φ1,・・・, φmを使って表したい、とする。すなわち、
x(t) = Σm Σi smi φm (t - τmi) + ε(t)
と書きたい(論文中式1)。(ε(t) は残差。)では、どのような kernel function を選べば、x(t) を最適に表現できるだろうか?
この問題に対して、音 x(t) が自然界の音であったり、人の声であったりするとき、学習アルゴリズムによって最適な kernel 関数の組をもとめる方法を開発したのが Lewicki NN 2002 論文みたい。これを彼らは「population spike code」と呼んだりしています。
それで、今回の論文では、この最適化学習アルゴリズムによって得られた kernel function と、ネコの auditory nerve の impulse response function(つまり生理学的データ)を比較してみたら、実にそっくりだった(Fig2a、赤(kernal)と青(実データ))、という話。つまり、auditory nerve の impulse response function は、自然界の音や音声などの音情報を伝達するのに、最適な kernel である、という結論。
(この論文では、auditory nerve の impulse response function を「revcor filter」と呼んでいるのですが、このあたりの話は僕は不勉強でよく知りません。。)
補足
Probabilistic Models of the Brain: Perception and Neural Function (eds Rao, Olshausen & Lewicki, MIT Press, 2002) の第12章にも、「population spike code」の話がありますね。
投稿者 sfujisawa : 22:13 | コメント (0)
2006年02月21日
Nature 2/2
GABA regulates synaptic integration of newly generated neurons in the adult brain
Shaoyu Ge, Eyleen L. K. Goh, Kurt A. Sailor, Yasuji Kitabatake, Guo-li Mingand Hongjun Song
今日のラボミーティングでシモルが文献紹介で使った論文。3 週間ぐらい前の論文なのだが、読み落としてたので軽くメモ。
アダルト Dentate Gyrus の新生 granule cell の maturation は、GABA カレントによってモジュレートされている、というはなし。マウス、スライスで、retrovirus を使って DG の proliferating cell に GFP を発現させる手法。
Perforant pathway を刺激すると、まだシナプスを形成していない 3 dpi (days post viral injection) の時点でも、脱分極方向の GABA カレントが流れる(Fig1)。で、GABA なのに脱分極方向に電流がながれるのは、immature の時点では GABA の 反転電位 EGABA が静止膜電位より浅いから(Fig2a)だが、Na-K-2Cl transporter NKCC1 を shRNA で knock down(この辺の手法の話はよく知りません)させると、immature でも EGABA は静止膜電位より浅くはならなかった(Fig2c)。
さらに、この NKCC1 knock down 状態では(つまり分極方向の GABA カレントが流れない状態では)、シナプス形成や dendrite 成長も阻害された、という話。
ちょっとよく分からなかったのは、28 dpi では、GABA の 反転電位 EGABA が既に静止膜電位より深くなっているはず(Fig2a)なのに、なんで Figure 1b では脱分極性の GABA カレントが流れているのだろう?
投稿者 sfujisawa : 20:47 | コメント (0)
2006年02月19日
Rauschenberg 展
いま、メトロポリタン美術館でラウシェンバーグ展をやっている。それで、1ヶ月ほど前に見に行って来たのだが、全く理解できなかった。。さすがネオ・ダダ。
くやしかったので、図録を買って勉強して、しかも同じ展覧会に計3回見に行った。それだけ見るとさすがに目が慣れてきて、ラウシェンバーグのすばらしさがだんだんと分かってきたわけであります。
☞ ☞ ☞
ロバート・ラウシェンバーグ (1925-) はテキサス出身の画家。最も活躍した時期は抽象表現主義(1950年代)とポップアート(1960年代)の間あたり。「ネオ・ダダ」と分類されている。
1950 年代は、抽象表現主義(ポロックやデ・クーニングなど)の全盛期で、「ニューヨーク派の勝利」といわれるほど評価されていたのだが、それに対して、ラウシェンバーグやジャスパー・ジョーンズは抽象表現主義を乗り越える試みを行う。彼らの目標は、生活と芸術との境界を取り払うことだったという。
ラウシェンバーグといえば、以下のエピソードが有名:
| 1953 年の秋、作家としての活動を始めてまだ間もないロバート・ラウシェンバーグは、21 歳も年上で既に抽象表現主義の代表的な作家としてゆるぎない名声を確立していたヴィレム・デ・クーニングの元を訪れた。ラウシェンバーグは尊敬する作家に向かってイメージを消すことによって作品を制作してみたいと提案し、デ・クーニングから一枚のドローイングを受けとった。そのドローイングは「本人さえも惜しいと思うほど重要であり、消すことが困難な作品」であったという。4 週間とも 6 週間ともいわれる長い期間、ラウシェンバーグは消しゴムでドローイングを拭き取ることを続け、ようやく最初に書かれていたドローイングが消失した。ラウシェンバーグはこの作品に「ロバート・ラウシェンバーグ作≪消されたデ・クーニングのドローイング≫ 1953 年」というキャプションをつけ、麗々しい金色の額縁の中に収めた。(「痕跡-過酷なる現実としての美術」尾崎信一郎 より) |
これがその作品。
さて、ラウシェンバーグは、1954 年あたりから、"Combines" と名付けられた一連の作品を作成し始める。今回の展覧会では、この Conbines シリーズのみを 67 点展示している。
この Combines シリーズの特徴は、
・新聞の切り抜きや写真や絵のコピーなどをカンバスを貼り付けてコラージュにする。
・さらに身の回りの生活用品(布団だの靴下だの時計だの)をカンバスに貼り付けている。
・そのうえに激しい筆致でペイントする。
例えばこの作品(Untitiled 1955)。カンバスにはメモ書きやら古めいた写真やら布きれやらニワトリのマグネットやらへんてこなヌード写真やらが無差別に貼り付けられて、画面からなんかすごい生活感の漂ってくる。その上から、抽象表現主義を思わせるような強い筆致でペイントすることにより、緊張感と調和が生まれるわけです。
こうした作品群は、身近な事物が素材になりうる、という新たなネタを美術界与えたわけで、若手画家たちに大きな影響を与えた。その結果、1960 年代に、ウォーホルとかリキテンシュタインとかを中心としたポップ・アートが生まれることになる。これが 50 年代から 60 年代にかけてのアメリカ美術の大まかな流れ。(ただ、ポップ・アート自体はラウシェンバーグの方向性とは別の方向に発展して行った。)
補足。
この写真、ラウシェンバーグの制作風景。手でベターっと絵の具(ペンキ?)を塗ってて、まさに抽象表現って感じ。こうしてみると、ラウシェンバーグは別に抽象表現主義を否定しようとしたのではなく、生活的なものと融合させたかった、ってことなんでしょうね。
投稿者 sfujisawa : 19:56 | コメント (0)
2006年02月17日
Multi taper (3)
昨日の続き。
なんとなく Matlab で簡単にコードが書けそうな気がしたので、試しに書いてみました。以下は、N=100 point、NW=5 の Multitaper を作るプログラムです。
|
N=100;W=0.05; for i=1:N [V,D]=eig(A); figure(1) figure(2) |
sinc 関数は matlab 関数で、sinc(t) = sin(pi*t)/(pi*t) です。t = 0 のとき sinc(0)=1 となることに注意。N が大きくなるとループ部が重たくなるので、
|
i=repmat(1:N,N,1); |
とした方がいいかもです。
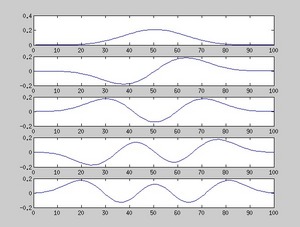
それで、固有ベクトルを固有値の大きいものから順に5つならべたのが以下の図です。Mitra 論文の Fig4 と同じ感じですね。これを窓関数として使えばいいのですね。
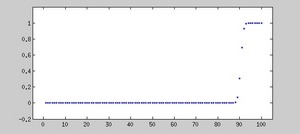
あと、固有値の分布を表示したのがその次の図です。固有値が小さい順に並んでいます。特徴は、大きいものから 2NW 番目(ここでは 2NW=10)までの固有値は、λ ~ 1 となり、それ以外は λ ~ 0 となる点です。
参考図書
Spectral Analysis for Physical Applications (Multitaper and conventional Univariate Techniques)
DB Percival and AT Walden, Cambridge Press, 1993
↑ アソハンがたまたま持ってた。Mitra 論文はこの本をベースにしてるみたい。
投稿者 sfujisawa : 20:32 | コメント (0)
2006年02月16日
Multi taper (2)
Analysis of Dynamic Brain Imaging Data
PP Mitra and B Pesaran
Biophys J , 1999,76:691-708.
昨日の続き。
ではどうやって Multi-taper を作るのか、ということだが、それは Mitra 論文の 「Analysis technique」の「Multitaper spectral analysis」という章に書いてある。しかし、この文章、省略されすぎてて何を書いてんのか理解できない。。かろうじで理解できたとこまでまとめてみます。(間違ってるかもしれません。)
--
あるデータ点数の Multi-taper の作成の仕方。
データの点数 : N
興味のある周波数領域 : [-W,W]
とする。NW=5 ぐらいになるように W を選ぶ。
ここで、(i,j) 成分が sin[2πW(i - j)] / π(i - j) である N×N 行列を Aij とするとき、
A v = λ v (論文中、式(9))
の固有方程式を解いて、その固有ベクトル v が Multi-taper らしい。
---
では、なぜ上述のような行列 Aij を選ぶのか。
(以下では、関数 v(t) をフーリエ変換したものを V(f)、関数 g(t) をフーリエ変換したものを G(f) と表記する)
Multi-taper は、スペクトルの周波数領域 [-W,W] を最適化するために設計された窓関数らしい。ここで、周波数領域で [-W,W] の矩形波関数 G(f) を考える。つまり、
G(f) = 1 (-W ≦ f ≦ W)
0 (elsewhere)
それで、
G(f) ・ V(f) = λ V(f) (λは正の整数)
を満たすような関数 V(f) があれば、この関数を窓関数として使うとき周波数領域 [-W,W] での power を最適化すると考えられる。
それで、一般的に、G(f) V(f) = g(t) * v(t) (ここで「*」は convolutionとする)という関係があるから、上の式は
∫ g(t-t')v(t')dt' = λ v(t)
と書き換えられる。ここで、g(t)、v(t) を離散値関数とすると、
Σt' g(t-t') v(t') = λ v(t)
となり、Aij = g(i-j) とすると、上述の固有方程式になる。
それで、ここがポイントなのだが、矩形波 G(f) のフーリエ逆変換は、
g(t) = sin (2πW t) / πt
となるらしいので、 Aij = sin[2πW(i - j)] / π(i - j) となる。
これででいいのかな?あんまり自信ない。
--
まあでも、上の固有方程式は Matlab なら eig 関数とかを使って簡単に解けるから、自分で multi-taper を作るのもそんなにめんどくさくはないかもね。
投稿者 sfujisawa : 19:58 | コメント (4)
2006年02月15日
Multi taper
Analysis of Dynamic Brain Imaging Data
PP Mitra and B Pesaran
Biophys J , 1999,76:691-708.
離散値フーリエ変換における Multi-taper method についての論文。
---
ブザキラボでは matlab での解析プログラムが蓄積されててとても便利である。(たとえば、ケン・ハリスがブザキラボ時代に書いたプログラム集「KenToolBox」はホームページで公開されていて、ここからダウンロードできる。)
これらのなかで、フーリエ変換を使う解析プログラムにはほぼすべてで「Multi-taper method」が使われている。(たとえば、KenToolBox にある mtpsg.m というコードでは Multi-taper を使って power spectrogram を作成する。)
これらのプログラムをただ使ってるだけなら別に問題ないのだが、先日、プログラムを少し改変しようと思ったところ、Multi-taper が何なのか分からずにつまづいてしまった。そこで、Multi-taper method について軽く勉強することにする。上の文献はアントンに教えてもらったもので、Multi-taper についての method 論文。
---
Multi-taper というのは、窓関数の一種らしい。窓関数といえば、Hamming Window とか Gaussian window とかが有名だが、Multi-taper では直交した複数の窓関数を用いる。
Multi-taper の窓関数の形は、こんな感じ(Mitra 論文の Fig4、左側の4つ)。それぞれの窓関数はお互いに直交している(つまり内積を計算すると 0 になる)。このそれそれの窓関数を使ってフーリエ変換した後に、得られたスペクトルを平均することによって、最終的なスペクトルを求める。
窓関数を使うのは、データ点数が比較的少なく、端点の影響が気になるときである。たとえば、2秒程度の長さのデータで FFT をして低周波成分(たとえば 3~8 Hzあたり)を注目するとき、どうしても端点の効果が気になる。このようなときは何らかの窓関数を用いた方が良いと思われる。データの長さが(注目する周波数に対して)とても長い場合は、べつに窓関数など用いなくてもふつうに FFT をすればよい。(窓関数に関してはこのページがけっこういい。Java が素敵。)
では普通の窓関数と比べて、 Multi-taper はどう良いのか。
<メリット(1)>
データ点数が少ないと低周波成分のデータが、どうしてもギザギザになってしまう。
たとえば、Mitra 論文の Fig5 に計算の途中経過が載っている。(Fig5 は Fig4 をそれぞれフーリエ変換したもの。)
見て分かるとおり、それぞれの窓関数で計算したデータはギザギザしてて、どれがノイズでどれが本当のピークか分かりづらい(Fig5の右側)。しかし、それぞれのデータを足しあわせて平均をとれば、ノイズ成分がとれてとても見やすくなる(Fig6)。ここで、それぞれの窓関数が直交している、というのがミソ。(直交しているからこそ、足しあわせによりノイズ成分が平坦化される。)
<メリット(2)>
窓関数を掛けてやると、端点近くでデータが0に押さえ込まれる分、power がある程度損失してしまう。しかし、Multi-taper method では、複数の窓関数を用いるために、窓関数の形に由来する Power の損失がある程度防げる。
<デメリット>
窓関数を作るのがめんどくさい。Hamming 窓や Gaussian 窓などは、自分の必要なデータ点数さえ決まればすぐに作ることができるが、Multi-taper の場合はいちいち固有方程式を解いて求めなければいけないので、自分で作ろうと思うとけっこう大変である。
つづく(かも)。
投稿者 sfujisawa : 20:54 | コメント (0)
2006年02月14日
ディスプレイ
うちのラボは今年はどうやら予算に余裕があったらしく、何個か液晶ディスプレイをまとめ買いしたみたい。それで、僕にもおこぼれで1つディスプレイが配給された。さっそく自分のノートパソコンにつないで、ダブル・ディスプレイにしてみたり。ちょっとうれしい。

投稿者 sfujisawa : 23:13 | コメント (0)
2006年02月12日
除雪
今年は記録的な暖冬とやらで、12月以来全く雪が降らなかった。しかし、昨日の夜から今日の昼にかけてひさびさに大雪が降る。今日の夕方には降り止んだものの、積雪量は40cmほどあり、歩くと膝の上まですっぽり雪に埋まってしまう。車もすっぽり雪に埋まってしまい、全く動かせない状態。しかたないので、近くの雑貨店で雪かきスコップを買ってきて雪かきを始める。
しかし、ひとりでやるので、雪をかけどもかけども全く減らない。4時間ほどやっても目標の半分ぐらいしかできてないので、相当へこんでいたところ、突然、除雪車がやってきて、うちのまわりの除雪を始めてくれだした。なんだ?かれらは神か?聞いてみると、どうやら彼らは、うちの家の1階の法律事務所(←今日は日曜なので休み)と契約している雪かき業者さんとのこと。なんだ、そんな人がいるなら早く言ってくれよ。。
彼らはさすがにプロなので、3人のスコップおにいさんと除雪車で、30分ほどできれいに除雪してくれた。僕の4時間の努力は何だったのだろう。。
↑ 除雪前(PM 5:00)、自力で除雪 (PM 9:00)、除雪屋さんが除雪 (PM 9:30)
投稿者 sfujisawa : 23:39 | コメント (0)
2006年02月08日
Nature 2/8
今日、ラボでとなりの席のアソハンがぼくのブログを偶然見つけて喜んでた。何かをググってたらひっかかったみたい。もちろん日本語だから彼は読めないのだけど、それでもちょっと恥ずかしかったり。
ところで、LINUX の firefox って、英語版でもちゃんと日本語文字が表示されるのでちょっとすごい。
Gamma-band synchronization in visual cortex predicts speed of change detection
Thilo Womelsdorf, Pascal Fries, Partha P. Mitraand Robert Desimone
Fries ラボ、Desimone ラボ。サル、V4 での local feild potential とマルチユニット(MUA)測定。データ自体は、Fries et al Science 2001 のときの実験データを使ってるらしく、解析しなおし論文みたい。
Fries 2001 では、attention により V4 での gamma 波が大きくなることを示していたが、今回の論文では、サルの reaction time と gamma 波の大きさ(および gamma-MUA coherence)が高い相関を持っていることを示している。
ところで、Fries の CV を見てみたら、 彼って 29 歳で PI として独立してますね。しかも、MD と PhD 両方持ってるし。どういうこと?
投稿者 sfujisawa : 19:55 | コメント (0)
2006年02月07日
Phys Rev Lett 2/10
Relation between Single Neuron and Population Spiking Statistics and Effects on Network Activity
Hideyuki Cateau and Alex D. Reyes
Reyes ラボの加藤英之さん。Synfire chain を Fokker-Plank 方程式で記述する、という内容。
Fokker-Plank 方程式は、確率密度の時間変化を記述する偏微分方程式です。
例えば t=0 で x=0 の点にいる粒子のブラウン運動を考えてみます。t=0 だと粒子の位置の確率密度分布はデルタ関数を用いて、p(x) = δ(x) とあらわされるでしょうが、t が大きくなるに従って次第に平べったい紡錘型の分布になることが想像できると思います。この p(x,t) を記述するのが Fokker-Planck 方程式です。(式の形は拡散方程式に似ています。)
それで、Reyes 2003 NN 論文の現象を数理的に記述するのが本論文の内容です。具体的には、N 個のニューロンを含む各 Layer での膜電位 Vm の確率分布 p(Vm, t) をFokker-Planck で記述するのが目的です。
(↑Reyes 論文は、ニューロンが synfire 的に feed-forward でつながっているとき、Layer 1 に Gaussian noise 入力を入れても、後方の Layer では Synfire 効果によりリズミックな出力が観察される、という論文。)
それで、今回の論文のポイントは、ニューロンの発火が、Poisson 過程ではないと仮定したところ。
これは、たぶん、Poisson 過程を仮定すると、うまくいかなかったためだと思う。何でうまくいかないかというと、ニューロンが Poisson 過程で発火するとすると、その inter-spike interval(ISI)は、指数分布に従う。つまり、t=0 のとこにピークが出るような分布。これを使うと、Fokker-Planck 方程式を解いたときに、Reyes 実験のような繰り替えし構造が出なかったのだと思う。(たぶん。)
(モデル細胞に、NMDA channel や NaP channel (persistent sodium channel) のような持続性のカレントを仮定すれば、たぶん解決できるのだろうが、ただ、それでは理論としての一般性がどうしても弱くなるので避けたと思われる。この論文では、モデル細胞にはもっともシンプルな leaky integrate-and-fire neuron を用いている。)
それで、neuron の ISI の分布形状を、指数分布ではなくガンマ分布であると仮定した。ISI 分布がガンマ分布であると仮定すると、その分布形状は実際のニューロンの ISI 分布と似たものになる。(たとえば 論文 Fig1a-middle)。
(ガンマ分布 Γ(α,σ) は α=1 のとき指数分布となることに注意。)
その仮定のもとで得られた Fokker-Planck 方程式が、式9(ノイズ入力が Gaussian noise のとき)あるいは式13(ノイズ入力が Gaussian noise でないとき)というわけです。
要約すると、各ニューロンの発火の ISI を、指数分布(←発火が Poisson 過程の場合)ではなくガンマ分布で近似すると、Reyes 論文の現象をうまく Fokker-Plank 方程式で記述できる、ということです。
投稿者 sfujisawa : 19:15 | コメント (0)
2006年02月06日
Neuron 2/2
Object Selectivity of Local Field Potentials and Spikes in the Macaque Inferior Temporal Cortex
Gabriel Kreiman, Chou P. Hung, Alexander Kraskov, Rodrigo Quian Quiroga, Tomaso Poggio, and James J. DiCarlo
Poggio が著者に入ってる。マカク IT 野での電気生理。Local field potential (LFP)の Object slectivity と、発火活動(おもに multi-unit activity)との関連について。(multi-unit activity とは、スパイクを単細胞に分離してなくてごちゃ混ぜの状態のこと。)LFP はその領域への "input" を反映していて、spike は "output" を反映している、という観点で書かれている。
IT 野は object selective なニューロンが存在する部位だが、LFP にも object selectivity がある程度存在するということを示した論文。
ぼく的には Figure6 がけっこう好き。LFP はどのくらいの距離内の発火活動に影響を与えているか、の算出をしている。電極を 1mm 毎に 10 本並べて(それぞれを電極1,電極2、・・とする)LFP と マルチユニットを記録しているのだが、その LFP と マルチユニットの correlation と距離の関係を解析している。具体的には、例えば、[Cutoff Distance = 3 mm] の場合、
「average of nearby sites (黒点)」では、電極1で記録された LFP と、電極1&2&3で記録されたマルチユニットの平均、との Correlation を計算する。
「avarage of remote sites(白点)」では、電極1の LFP と、電極4~10のマルチユニットの平均、との Correlation を計算する。それで、この2本の線が交わるのがだいたい 3 mm のところ。これより、LFP は 3mm 程度の距離内の細胞の発火(の平均)と関係している、ということを示唆してる。
投稿者 sfujisawa : 23:33 | コメント (0)
2006年02月03日
Science 2/3
最近ちょっと日記をさぼり気味。
WangXJの先週のJNS論文について書きたいのだけど、なんかうまく書けない。まあそのうち。
Rats Smell in Stereo
Raghav Rajan, James P. Clement, and Upinder S. Bhalla
匂い源の位置の特定に関する実験(Rat)。Rat での odor-localization task など。鼻を穴につっこむと右と左から空気が吹き付けられて、そのどちらかは匂い付き。右から空気が匂い付きなら右のノズルから水(報酬)がもらえて、左からの空気が匂い付きなら左から水がもらえるという task 。この task を、ラットは約6日の training で80~90%の正解率でできるみたい。あと、嗅球でのユニット記録もやっている(これは麻酔下)。嗅球では匂いの derection-selective な細胞がいるみたい。つまり、嗅球の時点ですでに匂い源の方向の分離ができているという話。